INTRODUCCIÓN
El papel desempeñado por los instrumentos ópticos en el advenimiento de la era contemporánea es raramente tomada en cuenta. Sin embargo, el telescopio ha sido decisivo en la afirmación del universo copernicano reclamado por Galileo. Sin las pruebas producidas por este instrumento durante la observación de los cuerpos celestes, el choque entre las concepciones geocéntrica y heliocéntrica podría haber continuado sin cesar. También el microscopio realiza una función similar revolucionario de la biología y la medicina, abriendo horizontes inmensos para ellos. Antes de la aparición de la cámara, las descripciones del mundo fueron producidos por artistas solamente. Eran representaciones valiosas en las que, sin embargo, la subjetividad del artista modificaba la realidad. La cámara presentó una forma mucho más dura de observar el mundo, pero mucho más objetiva.
Ya partir de estas consideraciones, es posible adivinar cuán grande es el papel desempeñado por los instrumentos ópticos y se encuentra en la formación del mundo que conocemos falta desde aqui va seguido. Estos instrumentos son perfectamente adecuados para la forma moderna y el objetivo de observar la realidad, pero ¿cómo funcionan? Hoy en día estamos en contacto continuo con instrumentos ópticos y sus productos. La comprensión de las propiedades de las lentes es fundamental para familiarizarse con estos instrumentos, para su uso de una manera creativa en el diseño de instrumentos ópticos. Esto es exactamente lo que haremos en los artículos siguientes y para ello es necesario tener un conocimiento básico de la óptica.
A partir de las descripciones teóricas complicadas en un libro de física, la comprensión de las propiedades de la lente no es fácil. Sin embargo, por medio de algunos experimentos sencillos en su lugar, es posible superar muchos obstáculos abstractos. En este punto, la física será más sencilla y eficaz.
A partir de las descripciones teóricas complicadas en un libro de física, la comprensión de las propiedades de la lente no es fácil. Sin embargo, por medio de algunos experimentos sencillos en su lugar, es posible superar muchos obstáculos abstractos. En este punto, la física será más sencilla y eficaz.
Hay dos tipos de lentes: los convergentes y los divergentes. Las lentes convergentes son capaces de converger la luz del sol hasta formar un disco pequeño y muy brillante que sea la imagen de nuestra estrella, mientras que las lentes divergentes divergir el haz de luz procedente del Sol por lo que su imagen no se puede formar. Aquí vamos a tratar sólo con los convergentes, que son más importantes. Los primeros experimentos que se realizan ahora tienen la intención de mostrar las principales propiedades de las lentes convergentes. Al final, a través del uso combinado de dos lentes, se muestran cómo funcionan algunos importantes instrumentos ópticos, tales como el telescopio y el microscopio.
Una lente convergente se puede utilizar de dos maneras: como un productor de imágenes y como una lupa.
Una lente convergente se puede utilizar de dos maneras: como un productor de imágenes y como una lupa.
La lente que produce imágenes
Equipo:
una lente convergente con distancia focal de entre 100 y 300 mm
una vela
una caja blanca
una regla de metro.
Puedes comprar los lentes en una tienda de óptica o fotografía.
Limpia una mesa y prepara un "banco óptico" como el que se muestra en la figura 1. Las distancias p y q debe ser mayor que la distancia focal del objetivo. Enciende la vela y apaga la luz. Modifica los valores de p y q, hasta que la imagen aparezca en la caja que se está utilizando como una pantalla. Realiza múltiples pruebas, cambiando las distancias. Prueba también el intercambio de las distancias p y q.
¿Cómo es la imagen que se forma? Para explicar esto, normalmente dos propiedades fundamentales de las lentes hay que tener en cuenta:
- Se desvía un haz de luz paralelo a su propio eje, y lo hace pasar por el centro;
- Se desvía un haz de luz paralelo a su propio eje, y lo hace pasar por el centro;
Con referencia a la figura 2, hay que tener en cuenta cualquier punto del objeto, para conveniencia el mas lejano. Entre todos los rayos de luz a partir de este momento, hay tres cuya trayectoria es particularmente fácil de seguir. El rayo A que pasa por el centro del objetivo y que no se desvía, el rayo B que llega a la lente se mueve paralelo al eje y que pasa a través de F1, el rayo C, que de una manera similar pasa a través de F2 y sale de la lente paralelo al el eje óptico. Estos tres rayos forman un punto de la imagen donde se cruzan entre sí.
Funciona de la misma manera para los puntos de otro objeto, para obtener la imagen completa. Para trazar estos diagramas, sólo dos de estos rayos son obligatorios. También hay otros rayos, no paralelos al eje y no pasan por los focos (f) de atención, y contribuyen a la formación de la imagen. También para estos sería posible calcular la trayectoria del rayo, pero para describir cómo funciona una lente, los que hemos tenido en cuenta es suficiente.
Durante este experimento, veremos que la imagen se forma invertida. Esto se puede explicar fácilmente siguiendo la trayectoria del rayo A. De hecho, un rayo a partir de una posición alta en el objeto, después de pasar por el centro del objetivo, se invertirá en el lado opuesto de la imagen.
AUMENTO DE UNA LENTE producir imágenes
Durante la realización de experimentos como los descritos en el párrafo anterior, debemos medir la altura del objeto y de su imagen (fig. 3). Dado que la llama de la vela no tiene una imagen estable podemos reemplazar la vela con un objeto bien iluminado preferentemenete por una lámpara como se muestra en la (figura 5). Es mejor de ser posible enmáscarar la luz dispersa de la lampara para que no pasa a través de la lente, a fin de obtener un mayor contraste y una imagen más visible
El tamaño de la imagen no es invariable, en el hecho de que la lente se mueve hacia el objeto, la imagen se mueve y se convierte en más grande (por lo tanto, debe mover la pantalla de distancia). El aumento viene dado por I = H / h, donde H es la altura de la imagen y la h es la del objeto.
No siempre es posible medir esas dimensiones. Por ejemplo, no puede abrir una cámara con la película en el interior, para medir la imagen. Es difícil incluso para medir muy distantes o demasiado pequeño un objeto. En estos casos, el aumento puede ser determinada mediante la medición de las distancias de P y Q. De hecho, para lentes delgadas, el rayo pasa a través del centro del objetivo y que no se desvía (fig. 3), contribuyen a formar dos triángulos semejantes que tienen un vértice común en el centro del objetivo. Sobre la base de las propiedades de los triángulos semejantes H/h = q/p, y, desde I=H / h, también I = q / p. se pueden verificar experimentalmente estas relaciónes.
Al traer la lente de la dirección del objeto iluminado, se llega a una posición en la que la imagen está muy lejos. Si la distancia del objeto lente es igual a la distancia focal, la imagen se formará en el infinito, mientras que un objeto colocado en el infinito, produce su propia imagen en el punto focal. Además, una lente colocada en 2F del objeto, se forma la imagen a la distancia 2F del mismo. En este caso, la proporción de aumento es igual a 1.
DETERMINACIÓN DE LA LONGITUD FOCAL
¿Cuál es la distancia focal? Esta palabra proviene del latín "focus" (fuego) de la propiedad de la lente para concentrar la luz del sol tanto como para prender fuego a objetos inflamables. La distancia desde la lente a la que los objetos deben mantenerse ha sido nombrada la longitud focal. En la óptica esta palabra se define como la distancia desde el nodo objetivo, hasta el punto en el que un rayo, que inicialmente fue paralelo al eje óptico, intercepta el eje después de haber sido desviado por la lente.
Para determinar la distancia focal de una lente convergente delgada, utilice de nuevo el implemento óptico especial (fig 1). Organiza el objeto iluminado y la lente, de tal manera que permitan obtener una imagen nítida en la pantalla. Medir la distancia p y q con la regla. La longitud focal está dada por:
Para determinar la distancia focal de una lente convergente delgada, utilice de nuevo el implemento óptico especial (fig 1). Organiza el objeto iluminado y la lente, de tal manera que permitan obtener una imagen nítida en la pantalla. Medir la distancia p y q con la regla. La longitud focal está dada por:
1 1 1 pxq --- = --- + --- En forma explícita: F = ------- PQP F + q
Para obtener una mejor aproximación, las mediciones deberán realizarse para calcular el valor promedio de la distancia focal del objetivo.
Distancia focal y DIOPTRÍAS
Hay otra forma de indicar la longitud focal de una lente. En los campos de la producción y el mercado de anteojos, en lugar de la distancia focal de la gente prefiere hablar de potencia de la lente, se mide en dioptrías. Por lo tanto, si usted tiene que comprar un lente de gafas, lo que necesita saber su poder. Distancia focal y la potencia de una lente están vinculados el uno al otro y se puede fácilmente pasar de una a la otra con esta sencilla fórmula:
D = 1/FL
donde:
D = dioptrías
FL = longitud focal del objetivo (expresada en metros!)
Además, se pone el signo "+" antes de una lente convergente y el signo "-" antes de una lente divergente.
Vamos a hacer un par de ejemplos:
- Una lente convergente de medio metro de distancia focal tiene una potencia de 2 dioptrías. De hecho: D = 1 / 0, 5 = 2
- Una lente divergente de 4 metros de distancia focal tiene una potencia de -0,25 dioptrías. De hecho: D = 1/-4 = -0,25
donde:
D = dioptrías
FL = longitud focal del objetivo (expresada en metros!)
Además, se pone el signo "+" antes de una lente convergente y el signo "-" antes de una lente divergente.
Vamos a hacer un par de ejemplos:
- Una lente convergente de medio metro de distancia focal tiene una potencia de 2 dioptrías. De hecho: D = 1 / 0, 5 = 2
- Una lente divergente de 4 metros de distancia focal tiene una potencia de -0,25 dioptrías. De hecho: D = 1/-4 = -0,25
La lupa
Equipo: una lente convergente con distancia focal comprendida entre 20 y 60 mm.
1) Observar a simple vista un objeto situado a una distancia de 250 mm;
2) observar el mismo objeto con el objetivo(lente) y comparar las dos imágenes.
La lente tiene que estar cerca de los ojos. Si se trata de planoconvex, mantener la superficie plana hacia el ojo. Enfoque el objeto hasta que se distinga.
Este experimento es muy simple. Pero, ¿cómo la lente magnifica el objeto?
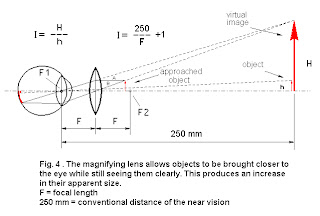
La distancia más cercana de visión a simple vista se considera que es 250 mm. Un hombre adulto normal tiene dificultad para ver claramente los objetos a menos de 250 mm. Lentes convergentes nos permite acercarnos al objeto muy por debajo de esta distancia y todavía lo vemos claro. Mientras nos acercamos al objeto veremos que es más grande (fig. 4). Un ojo humano es capaz de trabajar con luz paralela (de los objetos distantes) o con la luz de la divergencia limitado (no más cerca los objetos de 250 mm). Lentes convergentes reducen la divergencia de los rayos que nos da un objeto cercano a 250 mm, y nos permite aún ver claramente.
La distancia más cercana de visión a simple vista se considera que es 250 mm. Un hombre adulto normal tiene dificultad para ver claramente los objetos a menos de 250 mm. Lentes convergentes nos permite acercarnos al objeto muy por debajo de esta distancia y todavía lo vemos claro. Mientras nos acercamos al objeto veremos que es más grande (fig. 4). Un ojo humano es capaz de trabajar con luz paralela (de los objetos distantes) o con la luz de la divergencia limitado (no más cerca los objetos de 250 mm). Lentes convergentes reducen la divergencia de los rayos que nos da un objeto cercano a 250 mm, y nos permite aún ver claramente.
El objeto que se observa se debe colocar entre el foco (F2) y la lente (fig. 4). Para mayor comodidad se supone que el centro óptico del ojo coincide con el foco (F1) de la lente. (La distancia del ojo de la lente no es importante, pero en la práctica vamos a mantener el ojo cerca de la lente). Vamos a considerar un punto del objeto. Entre todos los rayos que dejan el objeto se dan por la conveniencia de rayos paralelos a un eje, que es desviado por la lente y pasa por el foco de nuevo F1 y llega a la retina. También tomarán rayos B que pasa por el centro del objetivo, que no se desvía y entra en el ojo pasa por la córnea e intercepta la retina, formando un punto de la imagen. La imagen formada en la retina se ve en un plano convencional a una distancia de 250 mm del ojo. No es una imagen real, en el sentido de que no se puede grabar en film y por esta razón se le llama virtual.
Esta imagen se percibe en la posición correcta, aunque en el ojo es al revés. Incluso cuando no estamos usando las lentes, las imágenes formadas en el ojo se invierten. Es el cerebro el que corrige esta imagen.
Esta imagen se percibe en la posición correcta, aunque en el ojo es al revés. Incluso cuando no estamos usando las lentes, las imágenes formadas en el ojo se invierten. Es el cerebro el que corrige esta imagen.
En el inicio de los rayos A y B tienen una gran divergencia, en el otro lado de la lente, la divergencia se reduce. Si el objeto se coloca en la F2, el objetivo sería hacer que los rayos A y B paralelos, para ver la imagen claramente, el ojo se centrará en el infinito. Por último, como decíamos, la lupa reduce la divergencia de la luz proveniente de un objeto cercano. El objetivo también permite que el objeto sea visto de forma clara y ampliada incluso por debajo de 250 mm.
Tenga en cuenta que la misma lente convergente puede ser utilizado tanto como una lupa y como un generador de imagen. Tenga en cuenta que el objetivo puede producir imágenes que se vuelve al revés, mientras que la lupa los mantiene en la posición correcta.
Tenga en cuenta que la misma lente convergente puede ser utilizado tanto como una lupa y como un generador de imagen. Tenga en cuenta que el objetivo puede producir imágenes que se vuelve al revés, mientras que la lupa los mantiene en la posición correcta.
En el caso de la lupa, la energía de la ampliación está determinada por la siguiente relación: I = 250 / F, donde F es la distancia focal del objetivo (mm) y 250 es la distancia convencional de visión distinta o la lectura. Por ejemplo, una lente de 50 mm de distancia focal se verá amplificada por 5 veces. Esto es útil cuando el ojo está enfocado en el infinito, mientras que cuando está enfocado para la visión cercana, la relación se convierte en I = (250 / F) 1. Por lo tanto, la lente de 50 mm de distancia focal aumenta 5-6 veces, según acomodación del ojo, por lo general una lupa no excede del 20 X.
Los instrumentos ópticos
Ahora ya estámos listos para la experiencia concluyente, el que debe permitir entender algunos de los trabajos más importantes de los instrumentos ópticos. Volvamos a la mesa óptica. Sin embargo, esta vez reemplazar la caja con una pantalla translúcida. Podemos hacerlo con un marco de carton en la que se han fijado un pedazo de plástico tomada a partir de una bolsa de plástico blanco (fig. 5). Enfocar la imagen en la pantalla y se puede observar la imagen que aparece por detrás de la pantalla.
Tambíen puede ampliar la imagen con una lupa, mediante la adopción de la lente que utilizó para el experimento anterior, y observando la imagen detrás de la pantalla translúcida. Como puede ver, la imagen aparece ampliada. Hasta el momento no hay nada extraño. Mientras continúan viendo la imagen al revés, tratar de mover la pantalla un poco. La imagen mantiene constante. Entonces ...
Hemos construido un telescopio! La lente más cercana del objeto es su objetivo, el mas cercano del ojo el ocular.
Con este experimento, sí el objetivo se acerca al objeto, la imagen se aleja y se hace más grande. Regula las distancias p y q de tal manera que la imagen se haga más grande que el objeto. Observa con la lupa: y de esta manera que habremos obtenido un microscopio compuesto (fig. 7)
Por lo tanto, lo que distingue a un microscopio de un telescopio. Como puedes ver, la estructura óptica es la misma, pero con telescopios de objetos estan distantes, mientras que en un microscopio que están cerca. Normalmente, un telescopio observa objetos ubicados a cientos de metros o más, y un microscopio observa objetos situados a unos pocos milímetros o menos de su objetivo.
La lente convergente puede:
- Producir una imagen real de un objeto;
- Aumentar las dimensiones aparentes de un objeto o una imagen;
- Ser utilizado con otros objetivos en la construcción de instrumentos ópticos.
- Producir una imagen real de un objeto;
- Aumentar las dimensiones aparentes de un objeto o una imagen;
- Ser utilizado con otros objetivos en la construcción de instrumentos ópticos.
Espero que estos sencillos experimentos hallan sido capaces de introducirlos al mundo de la óptica.
Esperamos que les haya gustado el experimento de hoy. Recuerda que puedes recibir GRATIS todos los experimentos y proyectos que vamos publicando, sólo tienes que suscribirte a nuestro feed rss, twitter o facebook, en la parte superior derecha.
Temas: ciencia, ciencias, experimento, experimentos, investigacion, proyecto, proyectos, física, óptica, de las lentes, instrumentos ópticos, teoria de la, aprender, entender, imagenes



















0 comentarios:
Publicar un comentario